Variance

In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its mean.

Variance definition

The variance of random variable X is the expected value of squares of difference of X and the expected value μ.

σ² = Var(X) = E[(X – μ)²]

From the definition of the variance we can get

σ² = Var(X) = E(X ²) – μ²

Variance of continuous random variable

For continuous random variable with mean value μ and probability density function f(x):

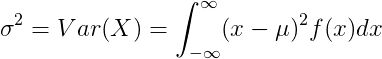or

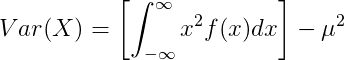Variance of discrete random variable

For discrete random variable X with mean value μ and probability mass function P(x):

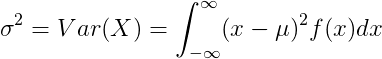or

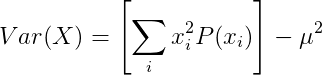Properties of variance

When X and Y are independent random variables:

Var(X+Y) = Var(X) + Var(Y)