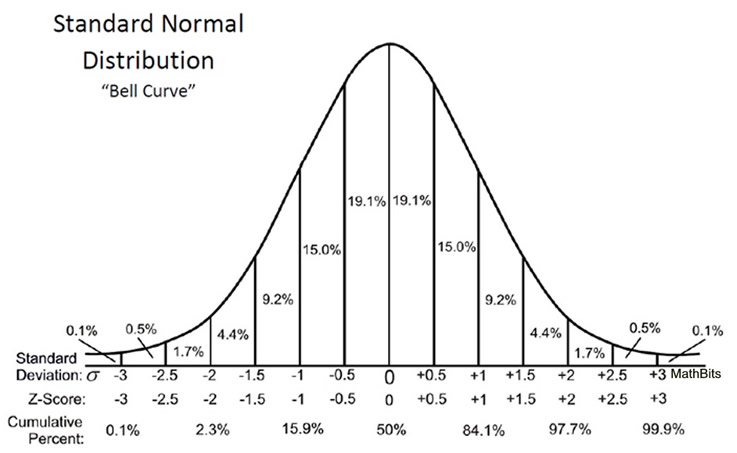
In probability theory, the normal (or Gaussian or Gauss or Laplace–Gauss) distribution is a very common continuous probability distribution. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. A random variable with a Gaussian distribution is said to be normally distributed and is called a normal deviate
The normal distribution is sometimes informally called the bell curve. However, many other distributions are bell-shaped (such as the Cauchy, Student’s t, and logistic distributions).
Normal distribution function
When random variable X has normal distribution,
X ∼ N (μ,σ2)
E (X) = μX
Var (X) = σ2X
The probability density function and cumulative distribution function of the normal distribution:
Probability density function (pdf)
The probability density function is given by:
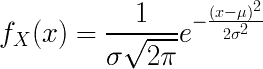 |
X is the random variable.
μ is the mean value.
σ is the standard deviation (std) value.
e = 2.7182818… constant.
π = 3.1415926… constant.
Cumulative distribution function
The cumulative distribution function is given by:
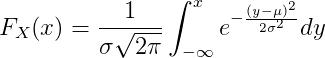 |
X is the random variable.
μ is the mean value.
σ is the standard deviation (std) value.
e = 2.7182818… constant.
π = 3.1415926… constant.
Standard normal distribution function
When
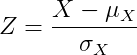 |
E(Z) = μz = 0
Var (Z) = σ2X = 1
Then the probability density function and cumulative distribution function of the standard normal distribution:
Probability density function
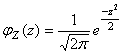 |
Cumulative distribution function
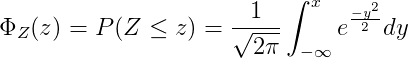 |
Standard normal distribution table
| z | Φ(z) | φ(z) |
| 0.00 | 0.5000 | 0.3989 |
| 0.01 | 0.5040 | 0.3989 |
| 0.02 | 0.5080 | 0.3989 |
| 0.03 | 0.5120 | 0.3988 |
| 0.04 | 0.5160 | 0.3986 |
| 0.05 | 0.5199 | 0.3984 |
| 0.06 | 0.5239 | 0.3982 |
| 0.07 | 0.5279 | 0.3980 |
| 0.08 | 0.5319 | 0.3977 |
| 0.09 | 0.5359 | 0.3973 |
| 0.10 | 0.5398 | 0.3970 |
| 0.11 | 0.5438 | 0.3965 |
| 0.12 | 0.5478 | 0.3961 |
| 0.13 | 0.5517 | 0.3956 |
| 0.14 | 0.5557 | 0.3951 |
| 0.15 | 0.5596 | 0.3945 |
| 0.16 | 0.5636 | 0.3939 |
| 0.17 | 0.5675 | 0.3932 |
| 0.18 | 0.5714 | 0.3925 |
| 0.19 | 0.5753 | 0.3918 |
| 0.20 | 0.5793 | 0.3910 |
| 0.21 | 0.5832 | 0.3902 |
| 0.22 | 0.5871 | 0.3894 |
| 0.23 | 0.5910 | 0.3885 |
| 0.24 | 0.5948 | 0.3876 |
| 0.25 | 0.5987 | 0.3867 |
| 0.26 | 0.6026 | 0.3857 |
| 0.27 | 0.6064 | 0.3847 |
| 0.28 | 0.6103 | 0.3836 |
| 0.29 | 0.6141 | 0.3825 |
| 0.30 | 0.6179 | 0.3814 |
| 0.31 | 0.6217 | 0.3802 |
| 0.32 | 0.6255 | 0.3790 |
| 0.33 | 0.6293 | 0.3778 |
| 0.34 | 0.6331 | 0.3765 |
| 0.35 | 0.6368 | 0.3752 |
| 0.36 | 0.6406 | 0.3739 |
| 0.37 | 0.6443 | 0.3725 |
| 0.38 | 0.6480 | 0.3712 |
| 0.39 | 0.6517 | 0.3697 |
| 0.40 | 0.6554 | 0.3683 |
| 0.41 | 0.6591 | 0.3668 |
| 0.42 | 0.6628 | 0.3653 |
| 0.43 | 0.6664 | 0.3637 |
| 0.44 | 0.6700 | 0.3621 |
| 0.45 | 0.6736 | 0.3605 |
| 0.46 | 0.6772 | 0.3589 |
| 0.47 | 0.6808 | 0.3572 |
| 0.48 | 0.6844 | 0.3555 |
| 0.49 | 0.6879 | 0.3538 |
| 0.50 | 0.6915 | 0.3521 |
| 0.51 | 0.6950 | 0.3503 |
| 0.52 | 0.6985 | 0.3485 |
| 0.53 | 0.7019 | 0.3467 |
| 0.54 | 0.7054 | 0.3448 |
| 0.55 | 0.7088 | 0.3429 |
| 0.56 | 0.7123 | 0.3410 |
| 0.57 | 0.7157 | 0.3391 |
| 0.58 | 0.7190 | 0.3372 |
| 0.59 | 0.7224 | 0.3352 |
| 0.60 | 0.7257 | 0.3332 |
| 0.61 | 0.7291 | 0.3312 |
| 0.62 | 0.7324 | 0.3292 |
| 0.63 | 0.7357 | 0.3271 |
| 0.64 | 0.7389 | 0.3251 |
| 0.65 | 0.7422 | 0.3230 |
| 0.66 | 0.7454 | 0.3209 |
| 0.67 | 0.7486 | 0.3187 |
| 0.68 | 0.7517 | 0.3166 |
| 0.69 | 0.7549 | 0.3144 |
| 0.70 | 0.7580 | 0.3123 |
| 0.71 | 0.7611 | 0.3101 |
| 0.72 | 0.7642 | 0.3079 |
| 0.73 | 0.7673 | 0.3056 |
| 0.74 | 0.7704 | 0.3034 |
| 0.75 | 0.7734 | 0.3011 |
| 0.76 | 0.7764 | 0.2989 |
| 0.77 | 0.7794 | 0.2966 |
| 0.78 | 0.7823 | 0.2943 |
| 0.79 | 0.7852 | 0.2920 |
| 0.80 | 0.7881 | 0.2897 |
| 0.81 | 0.7910 | 0.2874 |
| 0.82 | 0.7939 | 0.2850 |
| 0.83 | 0.7967 | 0.2827 |
| 0.84 | 0.7995 | 0.2803 |
| 0.85 | 0.8023 | 0.2780 |
| 0.86 | 0.8051 | 0.2756 |
| 0.87 | 0.8078 | 0.2732 |
| 0.88 | 0.8106 | 0.2709 |
| 0.89 | 0.8133 | 0.2685 |
| 0.90 | 0.8159 | 0.2661 |
| 0.91 | 0.8186 | 0.2637 |
| 0.92 | 0.8212 | 0.2613 |
| 0.93 | 0.8238 | 0.2589 |
| 0.94 | 0.8264 | 0.2565 |
| 0.95 | 0.8289 | 0.2541 |
| 0.96 | 0.8315 | 0.2516 |
| 0.97 | 0.8340 | 0.2492 |
| 0.98 | 0.8365 | 0.2468 |
| 0.99 | 0.8389 | 0.2444 |
| 1.00 | 0.8413 | 0.2420 |
| 1.01 | 0.8438 | 0.2396 |
| 1.02 | 0.8461 | 0.2371 |
| 1.03 | 0.8485 | 0.2347 |
| 1.04 | 0.8508 | 0.2323 |
| 1.05 | 0.8531 | 0.2299 |
| 1.06 | 0.8554 | 0.2275 |
| 1.07 | 0.8577 | 0.2251 |
| 1.08 | 0.8599 | 0.2227 |
| 1.09 | 0.8621 | 0.2203 |
| 1.10 | 0.8643 | 0.2179 |
| 1.11 | 0.8665 | 0.2155 |
| 1.12 | 0.8686 | 0.2131 |
| 1.13 | 0.8708 | 0.2107 |
| 1.14 | 0.8729 | 0.2083 |
| 1.15 | 0.8749 | 0.2059 |
| 1.16 | 0.8770 | 0.2036 |
| 1.17 | 0.8790 | 0.2012 |
| 1.18 | 0.8810 | 0.1989 |
| 1.19 | 0.8830 | 0.1965 |
| 1.20 | 0.8849 | 0.1942 |
| 1.21 | 0.8869 | 0.1919 |
| 1.22 | 0.8888 | 0.1895 |
| 1.23 | 0.8907 | 0.1872 |
| 1.24 | 0.8925 | 0.1849 |
| 1.25 | 0.8944 | 0.1826 |
| 1.26 | 0.8962 | 0.1804 |
| 1.27 | 0.8980 | 0.1781 |
| 1.28 | 0.8997 | 0.1758 |
| 1.29 | 0.9015 | 0.1736 |
| 1.30 | 0.9032 | 0.1714 |
| 1.31 | 0.9049 | 0.1691 |
| 1.32 | 0.9066 | 0.1669 |
| 1.33 | 0.9082 | 0.1647 |
| 1.34 | 0.9099 | 0.1626 |
| 1.35 | 0.9115 | 0.1604 |
| 1.36 | 0.9131 | 0.1582 |
| 1.37 | 0.9147 | 0.1561 |
| 1.38 | 0.9162 | 0.1539 |
| 1.39 | 0.9177 | 0.1518 |
| 1.40 | 0.9192 | 0.1497 |
| 1.41 | 0.9207 | 0.1476 |
| 1.42 | 0.9222 | 0.1456 |
| 1.43 | 0.9236 | 0.1435 |
| 1.44 | 0.9251 | 0.1415 |
| 1.45 | 0.9265 | 0.1394 |
| 1.46 | 0.9279 | 0.1374 |
| 1.47 | 0.9292 | 0.1354 |
| 1.48 | 0.9306 | 0.1334 |
| 1.49 | 0.9319 | 0.1315 |
| 1.50 | 0.9332 | 0.1295 |
| 1.51 | 0.9345 | 0.1276 |
| 1.52 | 0.9357 | 0.1257 |
| 1.53 | 0.9370 | 0.1238 |
| 1.54 | 0.9382 | 0.1219 |
| 1.55 | 0.9394 | 0.1200 |
| 1.56 | 0.9406 | 0.1182 |
| 1.57 | 0.9418 | 0.1163 |
| 1.58 | 0.9429 | 0.1145 |
| 1.59 | 0.9441 | 0.1127 |
| 1.60 | 0.9452 | 0.1109 |
| 1.61 | 0.9463 | 0.1092 |
| 1.62 | 0.9474 | 0.1074 |
| 1.63 | 0.9484 | 0.1057 |
| 1.64 | 0.9495 | 0.1040 |
| 1.65 | 0.9505 | 0.1023 |
| 1.66 | 0.9515 | 0.1006 |
| 1.67 | 0.9525 | 0.0989 |
| 1.68 | 0.9535 | 0.0973 |
| 1.69 | 0.9545 | 0.0957 |
| 1.70 | 0.9554 | 0.0940 |
| 1.71 | 0.9564 | 0.0925 |
| 1.72 | 0.9573 | 0.0909 |
| 1.73 | 0.9582 | 0.0893 |
| 1.74 | 0.9591 | 0.0878 |
| 1.75 | 0.9599 | 0.0863 |
| 1.76 | 0.9608 | 0.0848 |
| 1.77 | 0.9616 | 0.0833 |
| 1.78 | 0.9625 | 0.0818 |
| 1.79 | 0.9633 | 0.0804 |
| 1.80 | 0.9641 | 0.0790 |
| 1.81 | 0.9649 | 0.0775 |
| 1.82 | 0.9656 | 0.0761 |
| 1.83 | 0.9664 | 0.0748 |
| 1.84 | 0.9671 | 0.0734 |
| 1.85 | 0.9678 | 0.0721 |
| 1.86 | 0.9686 | 0.0707 |
| 1.87 | 0.9693 | 0.0694 |
| 1.88 | 0.9699 | 0.0681 |
| 1.89 | 0.9706 | 0.0669 |
| 1.90 | 0.9713 | 0.0656 |
| 1.91 | 0.9719 | 0.0644 |
| 1.92 | 0.9726 | 0.0632 |
| 1.93 | 0.9732 | 0.0620 |
| 1.94 | 0.9738 | 0.0608 |
| 1.95 | 0.9744 | 0.0596 |
| 1.96 | 0.9750 | 0.0584 |
| 1.97 | 0.9756 | 0.0573 |
| 1.98 | 0.9761 | 0.0562 |
| 1.99 | 0.9767 | 0.0551 |
| 2.00 | 0.9772 | 0.0540 |
| 2.01 | 0.9778 | 0.0529 |
| 2.02 | 0.9783 | 0.0519 |
| 2.03 | 0.9788 | 0.0508 |
| 2.04 | 0.9793 | 0.0498 |
| 2.05 | 0.9798 | 0.0488 |
| 2.06 | 0.9803 | 0.0478 |
| 2.07 | 0.9808 | 0.0468 |
| 2.08 | 0.9812 | 0.0459 |
| 2.09 | 0.9817 | 0.0449 |
| 2.10 | 0.9821 | 0.0440 |
| 2.11 | 0.9826 | 0.0431 |
| 2.12 | 0.9830 | 0.0422 |
| 2.13 | 0.9834 | 0.0413 |
| 2.14 | 0.9838 | 0.0404 |
| 2.15 | 0.9842 | 0.0396 |
| 2.16 | 0.9846 | 0.0387 |
| 2.17 | 0.9850 | 0.0379 |
| 2.18 | 0.9854 | 0.0371 |
| 2.19 | 0.9857 | 0.0363 |
| 2.20 | 0.9861 | 0.0355 |
| 2.21 | 0.9864 | 0.0347 |
| 2.22 | 0.9868 | 0.0339 |
| 2.23 | 0.9871 | 0.0332 |
| 2.24 | 0.9875 | 0.0325 |
| 2.25 | 0.9878 | 0.0317 |
| 2.26 | 0.9881 | 0.0310 |
| 2.27 | 0.9884 | 0.0303 |
| 2.28 | 0.9887 | 0.0297 |
| 2.29 | 0.9890 | 0.0290 |
| 2.30 | 0.9893 | 0.0283 |
| 2.31 | 0.9896 | 0.0277 |
| 2.32 | 0.9898 | 0.0270 |
| 2.33 | 0.9901 | 0.0264 |
| 2.34 | 0.9904 | 0.0258 |
| 2.35 | 0.9906 | 0.0252 |
| 2.36 | 0.9909 | 0.0246 |
| 2.37 | 0.9911 | 0.0241 |
| 2.38 | 0.9913 | 0.0235 |
| 2.39 | 0.9916 | 0.0229 |
| 2.40 | 0.9918 | 0.0224 |
| 2.41 | 0.9920 | 0.0219 |
| 2.42 | 0.9922 | 0.0213 |
| 2.43 | 0.9925 | 0.0208 |
| 2.44 | 0.9927 | 0.0203 |
| 2.45 | 0.9929 | 0.0198 |
| 2.46 | 0.9931 | 0.0194 |
| 2.47 | 0.9932 | 0.0189 |
| 2.48 | 0.9934 | 0.0184 |
| 2.49 | 0.9936 | 0.0180 |
| 2.50 | 0.9938 | 0.0175 |
| 2.51 | 0.9940 | 0.0171 |
| 2.52 | 0.9941 | 0.0167 |
| 2.53 | 0.9943 | 0.0163 |
| 2.54 | 0.9945 | 0.0158 |
| 2.55 | 0.9946 | 0.0154 |
| 2.56 | 0.9948 | 0.0151 |
| 2.57 | 0.9949 | 0.0147 |
| 2.58 | 0.9951 | 0.0143 |
| 2.59 | 0.9952 | 0.0139 |
| 2.60 | 0.9953 | 0.0136 |
| 2.61 | 0.9955 | 0.0132 |
| 2.62 | 0.9956 | 0.0129 |
| 2.63 | 0.9957 | 0.0126 |
| 2.64 | 0.9959 | 0.0122 |
| 2.65 | 0.9960 | 0.0119 |
| 2.66 | 0.9961 | 0.0116 |
| 2.67 | 0.9962 | 0.0113 |
| 2.68 | 0.9963 | 0.0110 |
| 2.69 | 0.9964 | 0.0107 |
| 2.70 | 0.9965 | 0.0104 |
| 2.71 | 0.9966 | 0.0101 |
| 2.72 | 0.9967 | 0.0099 |
| 2.73 | 0.9968 | 0.0096 |
| 2.74 | 0.9969 | 0.0093 |
| 2.75 | 0.9970 | 0.0091 |
| 2.76 | 0.9971 | 0.0088 |
| 2.77 | 0.9972 | 0.0086 |
| 2.78 | 0.9973 | 0.0084 |
| 2.79 | 0.9974 | 0.0081 |
| 2.80 | 0.9974 | 0.0079 |
| 2.81 | 0.9975 | 0.0077 |
| 2.82 | 0.9976 | 0.0075 |
| 2.83 | 0.9977 | 0.0073 |
| 2.84 | 0.9977 | 0.0071 |
| 2.85 | 0.9978 | 0.0069 |
| 2.86 | 0.9979 | 0.0067 |
| 2.87 | 0.9979 | 0.0065 |
| 2.88 | 0.9980 | 0.0063 |
| 2.89 | 0.9981 | 0.0061 |
| 2.90 | 0.9981 | 0.0060 |
| 2.91 | 0.9982 | 0.0058 |
| 2.92 | 0.9982 | 0.0056 |
| 2.93 | 0.9983 | 0.0055 |
| 2.94 | 0.9984 | 0.0053 |
| 2.95 | 0.9984 | 0.0051 |
| 2.96 | 0.9985 | 0.0050 |
| 2.97 | 0.9985 | 0.0048 |
| 2.98 | 0.9986 | 0.0047 |
| 2.99 | 0.9986 | 0.0046 |
| 3.00 | 0.9987 | 0.0044 |
| 3.01 | 0.9987 | 0.0043 |
| 3.02 | 0.9987 | 0.0042 |
| 3.03 | 0.9988 | 0.0040 |
| 3.04 | 0.9988 | 0.0039 |
| 3.05 | 0.9989 | 0.0038 |
| 3.06 | 0.9989 | 0.0037 |
| 3.07 | 0.9989 | 0.0036 |
| 3.08 | 0.9990 | 0.0035 |
| 3.09 | 0.9990 | 0.0034 |
| 3.10 | 0.9990 | 0.0033 |
| 3.11 | 0.9991 | 0.0032 |
| 3.12 | 0.9991 | 0.0031 |
| 3.13 | 0.9991 | 0.0030 |
| 3.14 | 0.9992 | 0.0029 |
| 3.15 | 0.9992 | 0.0028 |
| 3.16 | 0.9992 | 0.0027 |
| 3.17 | 0.9992 | 0.0026 |
| 3.18 | 0.9993 | 0.0025 |
| 3.19 | 0.9993 | 0.0025 |
| 3.20 | 0.9993 | 0.0024 |
| 3.21 | 0.9993 | 0.0023 |
| 3.22 | 0.9994 | 0.0022 |
| 3.23 | 0.9994 | 0.0022 |
| 3.24 | 0.9994 | 0.0021 |
| 3.25 | 0.9994 | 0.0020 |
| 3.26 | 0.9994 | 0.0020 |
| 3.27 | 0.9995 | 0.0019 |
| 3.28 | 0.9995 | 0.0018 |
| 3.29 | 0.9995 | 0.0018 |
| 3.30 | 0.9995 | 0.0017 |
| 3.31 | 0.9995 | 0.0017 |
| 3.32 | 0.9995 | 0.0016 |
| 3.33 | 0.9996 | 0.0016 |
| 3.34 | 0.9996 | 0.0015 |
| 3.35 | 0.9996 | 0.0015 |
| 3.36 | 0.9996 | 0.0014 |
| 3.37 | 0.9996 | 0.0014 |
| 3.38 | 0.9996 | 0.0013 |
| 3.39 | 0.9997 | 0.0013 |
| 3.40 | 0.9997 | 0.0012 |
| 3.41 | 0.9997 | 0.0012 |
| 3.42 | 0.9997 | 0.0012 |
| 3.43 | 0.9997 | 0.0011 |
| 3.44 | 0.9997 | 0.0011 |
| 3.45 | 0.9997 | 0.0010 |
| 3.46 | 0.9997 | 0.0010 |
| 3.47 | 0.9998 | 0.0010 |
| 3.48 | 0.9998 | 0.0009 |
| 3.49 | 0.9998 | 0.0009 |
| 3.50 | 0.9998 | 0.0009 |
| 3.51 | 0.9998 | 0.0008 |
| 3.52 | 0.9998 | 0.0008 |
| 3.53 | 0.9998 | 0.0008 |
| 3.54 | 0.9998 | 0.0008 |
| 3.55 | 0.9998 | 0.0007 |
| 3.56 | 0.9998 | 0.0007 |
| 3.57 | 0.9998 | 0.0007 |
| 3.58 | 0.9998 | 0.0007 |
| 3.59 | 0.9998 | 0.0006 |
| 3.60 | 0.9998 | 0.0006 |
| 3.61 | 0.9998 | 0.0006 |
| 3.62 | 0.9999 | 0.0006 |
| 3.63 | 0.9999 | 0.0005 |
| 3.64 | 0.9999 | 0.0005 |
| 3.65 | 0.9999 | 0.0005 |
| 3.66 | 0.9999 | 0.0005 |
| 3.67 | 0.9999 | 0.0005 |
| 3.68 | 0.9999 | 0.0005 |
| 3.69 | 0.9999 | 0.0004 |
| 3.70 | 0.9999 | 0.0004 |
| 3.71 | 0.9999 | 0.0004 |
| 3.72 | 0.9999 | 0.0004 |
| 3.73 | 0.9999 | 0.0004 |
| 3.74 | 0.9999 | 0.0004 |
| 3.75 | 0.9999 | 0.0004 |
| 3.76 | 0.9999 | 0.0003 |
| 3.77 | 0.9999 | 0.0003 |
| 3.78 | 0.9999 | 0.0003 |
| 3.79 | 0.9999 | 0.0003 |
| 3.80 | 0.9999 | 0.0003 |
| 3.81 | 0.9999 | 0.0003 |
| 3.82 | 0.9999 | 0.0003 |
| 3.83 | 0.9999 | 0.0003 |
| 3.84 | 0.9999 | 0.0003 |
| 3.85 | 0.9999 | 0.0002 |
| 3.86 | 0.9999 | 0.0002 |
| 3.87 | 0.9999 | 0.0002 |
| 3.88 | 0.9999 | 0.0002 |
| 3.89 | 0.9999 | 0.0002 |
| 3.90 | 1.0000 | 0.0002 |
| 3.91 | 1.0000 | 0.0002 |
| 3.92 | 1.0000 | 0.0002 |
| 3.93 | 1.0000 | 0.0002 |
| 3.94 | 1.0000 | 0.0002 |
| 3.95 | 1.0000 | 0.0002 |
| 3.96 | 1.0000 | 0.0002 |
| 3.97 | 1.0000 | 0.0002 |
| 3.98 | 1.0000 | 0.0001 |
| 3.99 | 1.0000 | 0.0001 |
Standard Normal Distribution Graph