Basic Probability Formulas

In this article we will learn basic probability formulas.

Probability Range:

0 ≤ P(A) ≤ 1

Rule of Complementary Events:

P(A^C) + P(A) = 1

Rule of Addition:

P(A∪B) = P(A) + P(B) – P(A∩B)

Disjoint Events:

Events A and B are disjoint iff
P(A∩B) = 0

Conditional Probability:

P(A | B) = P(A∩B) / P(B)

Bayes Formula:

P(A | B) = P(B | A) ⋅ P(A) / P(B)

Independent Events:

Events A and B are independent iff
P(A∩B) = P(A) ⋅ P(B)

Cumulative Distribution Function:

F_X(x) = P(X ≤ x)

Cumulative Distribution Function:

F_X(x) = P(X ≤ x)

Probability Mass Function:

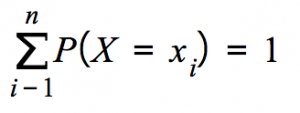Probability Density Function:

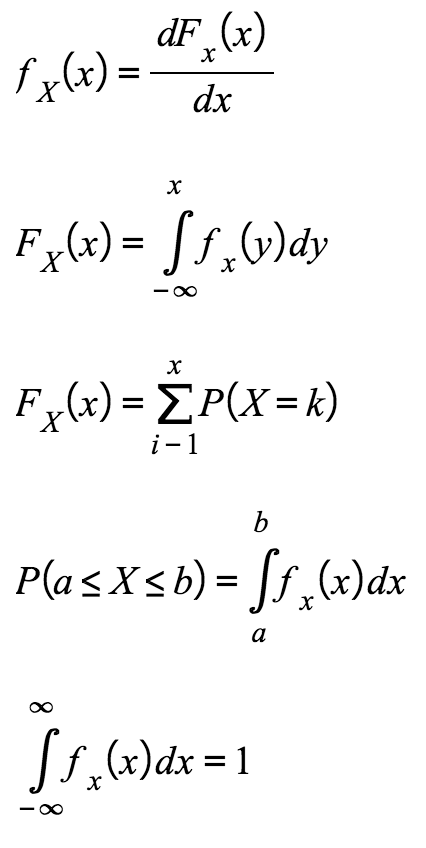Covariance:

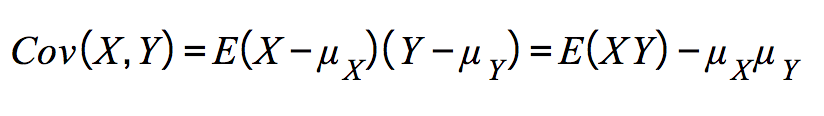Correlation:

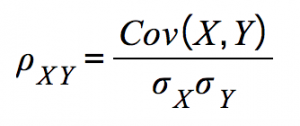Bernoulli: 0-failure 1-success

Geometric: 0-failure 1-success

Hypergeometric: N objects with K success objects, n objects are taken.