Zero number definition
Zero is a number used in mathematics to describe no quantity or null quantity.
When there are 2 apples on the table and we take the 2 apples, we can say that there are zero apples on the table.
The zero number is not positive number and not negative number.
The zero is also a placeholder digit in other numbers (e.g: 40,103, 170).
Is zero a number?
Zero is a number. It is not positive nor negative number.
Zero digit
The zero digit is used as a placeholder when writing numbers.
For example:
204 = 2×100+0×10+4×1
Zero number history
Who invented the zero number?
The modern 0 symbol was invented in India in the 6-th century, used later by the Persians and Arabs and later in Europe.
Symbol of zero
The zero number is denoted with the 0 symbol.
The Arabic numeral system uses the ٠ symbol.
Zero number properties
x represents any number.
| Operation | Rule | Example |
| Addition | x + 0 = x | 3 + 0 = 3 |
| Subtraction | x - 0 = x | 3 - 0 = 3 |
| Multiplication | x × 0 = 0 | 5 × 0 = 0 |
| Division | 0 ÷ x = 0 , when x ≠ 0 | 0 ÷ 5 = 0 |
| x ÷ 0 is undefined | 5 ÷ 0 is undefined | |
| Exponentiation | 0 x = 0 | 05 = 0 |
| x 0 = 1 | 50 = 1 | |
| Root | √0 = 0 | |
| Logarithm | logb(0) is undefined | |
| Factorial | 0! = 1 | |
| Sine | sin 0º = 0 | |
| Cosine | cos 0º = 1 | |
| Tangent | tan 0º = 0 | |
| Derivative | 0' = 0 | |
| Integral | ∫ 0 dx = 0 + C | |
Zero addition
Addition of a number plus zero is equal to the number:
x + 0 = x
For example:
7 + 0 = 7
Zero subtraction
Subtraction of a number minus zero is equal to the number:
x – 0 = x
For example:
7 – 0 = 7
Multiplication by zero
Multiplication of a number times zero is equal to zero:
x × 0 = 0
For example:
7 × 0 = 0
Number divided by zero
Division of a number by zero is not defined:
x ÷ 0 is undefined
For example:
7 ÷ 0 is undefined
Zero divided by a number
Division of a zero by a number is zero:
0 ÷ x = 0
For example:
0 ÷ 7 = 0
Number to the zero power
The power of a number raised by zero is one:
x0 = 1
For example:
70 = 1
Logarithm of zero
The base b logarithm of zero is undefined:
logb(0) is undefined
There is no number we can raise the base b with to get zero.
Only the limit of the base b logarithm of x, when x converges zero is minus infinity:
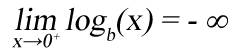 Sets that contain zero
Sets that contain zero
Zero is an element of the natural numbers, integer numbers, real numbers and complex numbers sets:
| Set | Set membership notation |
| Natural numbers (non negative) | 0 ∈ ℕ0 |
| Integer numbers | 0 ∈ ℤ |
| Real numbers | 0 ∈ ℝ |
| Complex numbers | 0 ∈ ℂ |
| Rational numbers | 0 ∈ ℚ |
Is zero even or odd number?
The set of even numbers is:
{… , -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, …}
The set of odd numbers is:
{… ,-9, -7, -5, -3, -1, 1, 3, 5, 7, 9, …}
Zero is an integer multiple of 4:
0 × 4 = 0
Zero is a member of the even numbers set:
0 ∈ {2k, k∈ℤ}
So zero is an even number and not an odd number.
Is zero a natural number?
There are two definitions for the natural numbers set.
The set of non negative integers:
ℕ0 = {0,1,2,3,4,5,6,7,8,…}
The set of positive integers:
ℕ1 = {1,2,3,4,5,6,7,8,…}
Zero is a member of the set of non negative integers:
0 ∈ ℕ0
Zero is not a member of the set of positive integers:
0 ∉ ℕ1
Is zero a whole number?
There are three definitions for the whole numbers:
The set of integer numbers:
ℤ = {0,1,2,3,4,5,6,7,8,…}
The set of non negative integers:
ℕ0 = {0,1,2,3,4,5,6,7,8,…}
The set of positive integers:
ℕ1 = {1,2,3,4,5,6,7,8,…}
Zero is a member of the set of integer numbers and the set of non negative integers:
0 ∈ ℤ
0 ∈ ℕ0
Zero is not a member of the set of positive integers:
0 ∉ ℕ1
Is zero an integer number?
The set of integer numbers:
ℤ = {0,1,2,3,4,5,6,7,8,…}
Zero is a member of the set of integer numbers:
0 ∈ ℤ
So zero is an integer number.
Is zero a rational number?
A rational number is a number that can be expressed as the quotient of two integer numbers:
ℚ = {n/m; n,m∈ℤ}
Zero can be written as a quotient of two integer numbers.
For example:
0 = 0/7
So zero is a rational number.
Is zero a positive number?
A positive number is defined as a number that is greater than zero:
x > 0
For example:
7 > 0
Since zero is not greater than zero, it is not a positive number.
Is zero a prime number?
The number 0 is not a prime number.
Zero is not a positive number and has infinite number of divisors.
The lowest prime number is 2.
