Exponent rules, laws of exponent and examples.
What is an exponent
The base a raised to the power of n is equal to the multiplication of a, n times:
an = a × a × … × a (n times)
a is the base and n is the exponent.
Examples
31 = 3
32 = 3 × 3 = 9
33 = 3 × 3 × 3 = 27
34 = 3 × 3 × 3 × 3 = 81
35 = 3 × 3 × 3 × 3 × 3 = 243
310 = 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 = 59 049
Exponents rules and properties
| Rule name | Rule | Example |
| Product rules | a n ⋅ a m = a n+m | 23 ⋅ 24 = 23+4 = 128 |
| a n ⋅ b n = (a ⋅ b) n | 32 ⋅ 42 = (3⋅4)2 = 144 | |
| Quotient rules | a n / a m = a n-m | 25 / 23 = 25-3 = 4 |
| a n / b n = (a / b) n | 43 / 23 = (4/2)3 = 8 | |
| Power rules | (bn)m = bn⋅m | (23)2 = 23⋅2 = 64 |
| bnm = b(nm) | 232 = 2(32) = 512 | |
| m√(bn) = b n/m | 2√(26) = 26/2 = 8 | |
| b1/n = n√b | 81/3 = 3√8 = 2 | |
| Negative exponents | b-n = 1 / bn | 2-3 = 1/23 = 0.125 |
| Zero rules | b0 = 1 | 50 = 1 |
| 0n = 0 , for n>0 | 05 = 0 | |
| One rules | b1 = b | 51 = 5 |
| 1n = 1 | 15 = 1 | |
| Minus one rule | 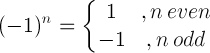 | (-1)5 = -1 |
| Derivative rule | (xn)' = n⋅x n-1 | (x3)' = 3⋅x3-1 |
| Integral rule | ∫ xndx = xn+1/(n+1)+C | ∫ x2dx = x2+1/(2+1)+C |
Exponents product rules
Product rule with same base
an ⋅ am = an+m
Example:
22 ⋅ 23 = 22+3 = 25 = 2⋅2⋅2⋅2⋅2 = 32
Product rule with same exponent
an ⋅ bn = (a ⋅ b)n
Example:
22 ⋅ 32 = (2⋅3)2 = 62 = 6⋅6 = 36
Exponents quotient rules
Quotient rule with same base
an / am = an-m
Example:
24 / 22 = 24-2 = 22 = 2⋅2 = 4
Quotient rule with same exponent
an / bn = (a / b)n
Example:
63 / 33 = (6/3)3 = 23 = 2⋅2⋅2 = 8
Exponents power rules
Power rule I
(an) m = a n⋅m
Example:
(21)3 = 21⋅3 = 23 = 2⋅2⋅2 = 8
Power rule II
a nm = a (nm)
Example:
232 = 2(32) = 2(3⋅3) = 29 = 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512
Power rule with radicals
m√(a n) = a n/m
Example:
2√(26) = 26/2 = 23 = 2⋅2⋅2 = 8
Negative exponents rule
b-n = 1 / bn
Example:
2-3 = 1/23 = 1/(2⋅2⋅2) = 1/8 = 0.125
